Deep Residual Learning for Image Recognition
Deeper neural networks are more difficult to train. Residual learning framework allows training much deeper networks. The layers in this framework are reformulated as learning residual functions with reference to the layer inputs, instead of learning unreferenced functions.
Intuition
Deep neural networks naturally integrate low/middle/high-level features and classifiers in an end-to-end multilayer fashion. The levels of features can be enriched by the number of stacked layers. VGG and Inception modules reveal that the network depth is of crucial importance.
One of the problems in training very deep neural networks is the problem of vanishing/exploding gradients, which hamper convergence from the beginning. This problem has been addressed by normalized initialization and normalization of intermediate layers (called batch normalization).
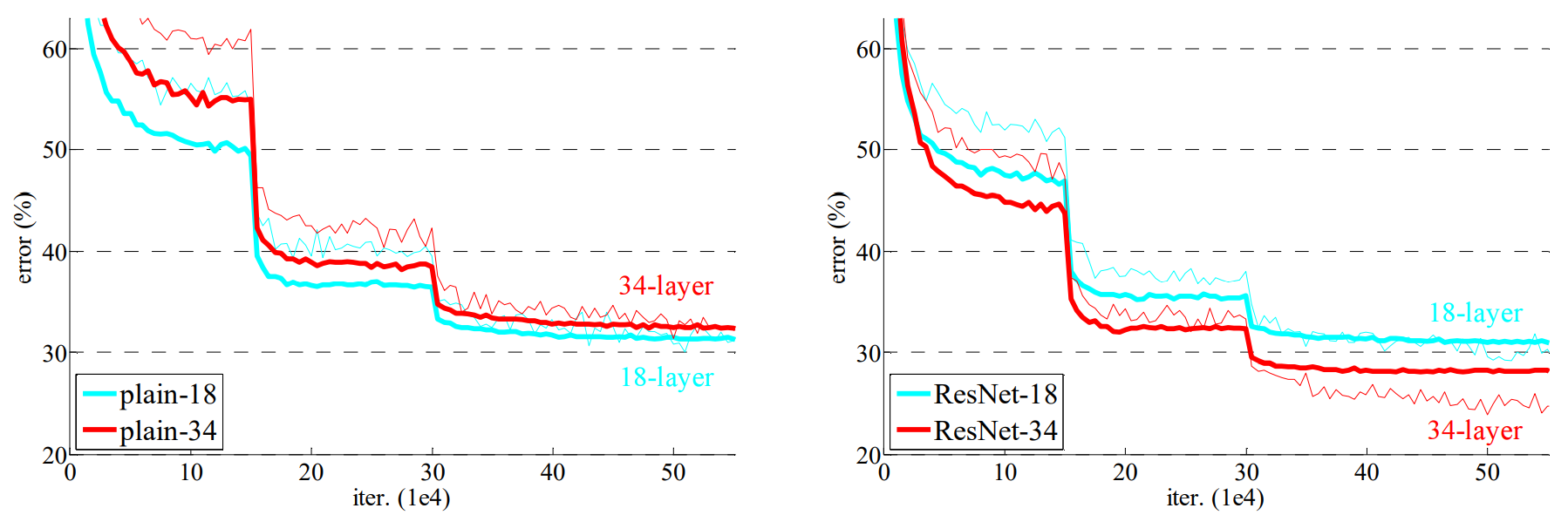
However, when deeper networks are able to start converging, a degradation problem get in the way. Network degradation problem makes the accuracy get saturated when the depth of the network increases. Such degradation is not caused by overfitting, and adding more layers after a certain threshold leads to higher training error.
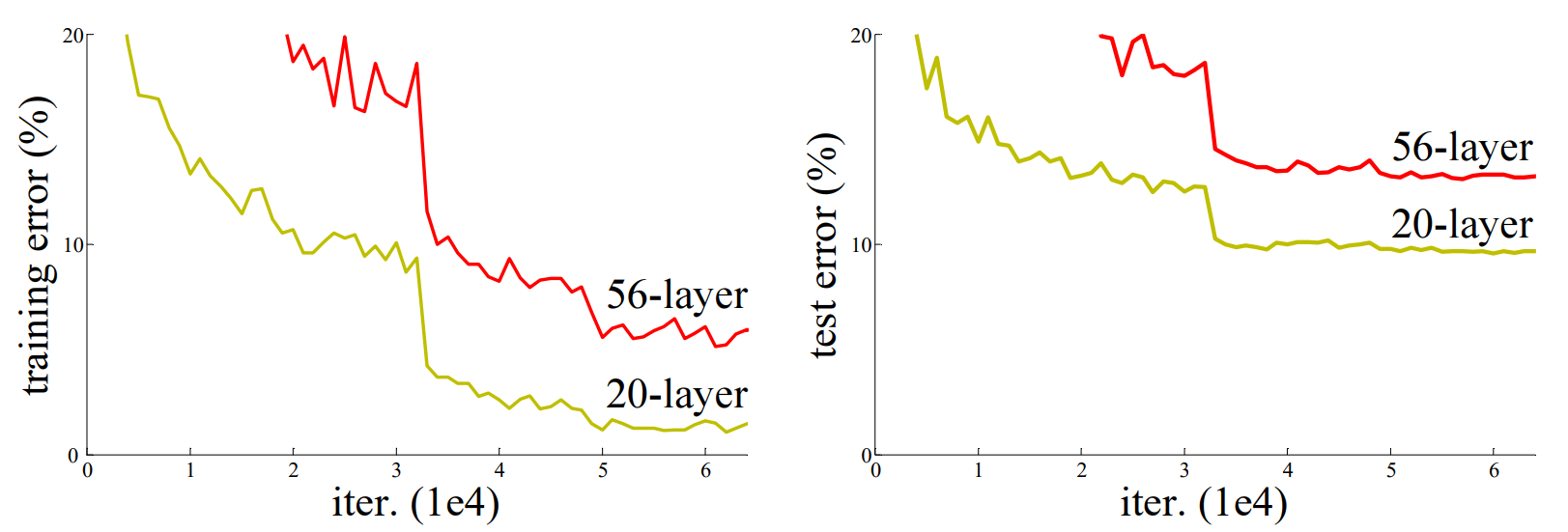
Comparing with shallower counterpart, a deeper model can potentially learn the identity mapping for the added layers, while the other layers are copied from the shallower model. This solution indicated that a deeper model should produce no higher training error than its shallower counterpart.
The problem suggests that the solvers might have difficulties in approximating identity mappings by multiple nonlinear layers. If the identity mappings are optimal, the solvers can zero-out the weights of multiple non-linear layers to approach identity mappings. In real cases identity mappings are unlikely to be optimal, but the reformulation may help to precondition the problem.
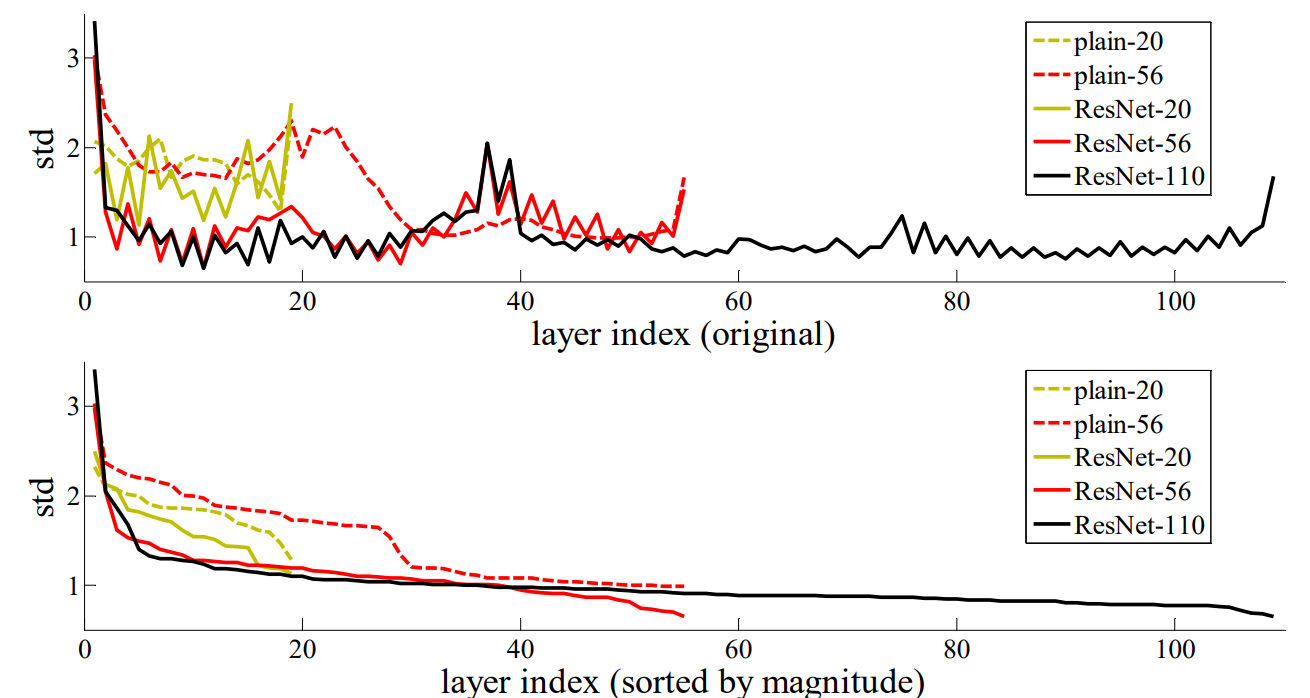
The evidence for reasonable preconditioning is the small responses of the learned residual functions. ResNets have generally smaller responses than their plain counterparts. The residual functions might be generally closer to zero than the non-residual functions. When there are more layers, an individual layer tends to modify the signal less.
Inspiration
VLAD and Fisher Vector encode a representation by the residual vectors with respect to a dictionary. Encoding residual vectors has been shown to be more effective than encoding original vectors.
Multigrid method solves Partial Differential Equations as subproblems with residual solutions between a coarser and a finer scale. A hierarchical basis preconditioning, an alternative to the Multigrid method, relies on variables that represent residual vectors between two scales. Both solvers converge much faster than standard solvers that are unaware of the residual nature of the solutions.
An early practice of training multi-layer perceptrons is to add a linear layer connected from the network input to the output. Intermediate layers in some models are connected to auxiliary classifiers for addressing vanishing/exploding gradients. Inception layer is composed of a shortcut branch.
Highway networks use shortcut connections with gated functions. The gates are learnable and can be closed, so that the layers can become non-residual functions.
Residual learning
Let \(H(x)\) denote an underlying mapping to be fit by a few stacked layers with \(x\) denoting the inputs to the first of these layers. If one hypothesize that multiple nonlinear layers can asymptotically approximate complicated functions, then it is equivalent to hypothesize that they can asymptotically approximate the residual functions \(H(x)-x\) (assuming the input and output are of the same dimensions).
Therefore, rather than expect stacked layers to approximate \(H(x)\), they can be allowed to approximate a residual function \(F(x)=H(x)-x\). Thus, the original function becomes \(F(x)+x\). Although both forms should be able to asymptotically approximate the desired functions, the ease of learning might be different.
Such formulation can be realized by feedforward neural networks with shortcut connections. The shortcut connections simply perform identity mapping, and their outputs are added to the outputs of the stacked layers.
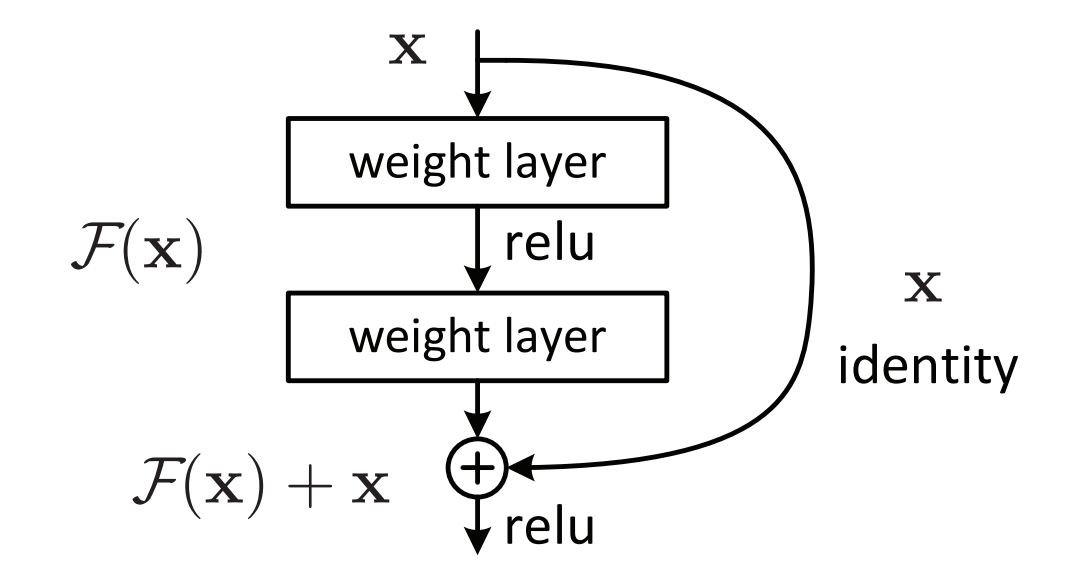
The authors emphasize that when the desired mapping \(H(x)\) is an identity mapping \(H(x)=x\), then \(F(x)=H(x)-x\) becomes the residual.
Architecture
Residual learning is adopted to every few stacked layers. A building block is defined as the following:
$$y = F(x,\{W_i\}) + x,$$
where \(x\) and \(y\) are the input and output vectors of the layers considered. The function \(F(x,\{W_i\})\) represents the residual mapping to be learned. The residual mapping has two layers, \(F=W_2\sigma (W_1 x)\) where \(\sigma\) denotes ReLU, and biases are omitted. The operation \(F+x\) is performed by a shortcut connection and element-wise addition. The second nonlinearity is applied after the addition.
The shortcut connection does not introduce any new parameters or additional computational complexity.
The dimensions of \(x\) and \(F\) must be equal for the previous equation to work. If this is not the case, a linear projection \(W_S\) can be performed on the shortcut connections to match the dimensions:
$$y = F(x,\{W_i\}) + W_S x$$
The form of residual function \(F\) is flexible. In the proposed architectures, two or three layers were used, but more layers are possible. However, if \(F\) has only a single layer, it becomes similar to a linear layer with no additional benefits. The notation is applicable to fully connected layers, as well as to convolutional layers. For convolutional layers, the function \(F(x,\{W_i\})\) can represent multiple convolutional layers. The element-wise addition is performed on two feature maps, channel by channel.
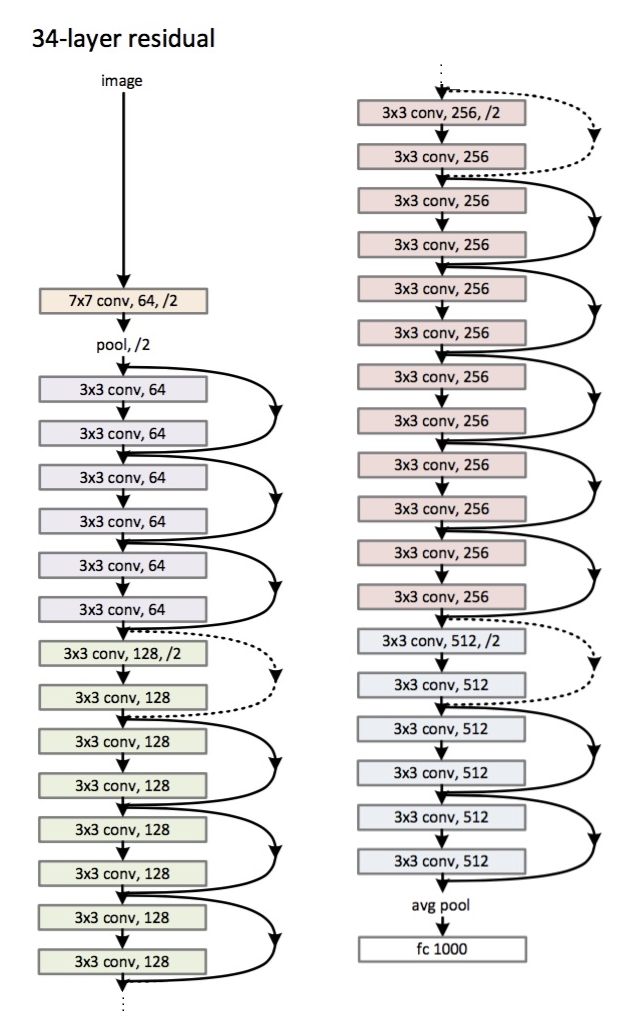
Solid lines represent the shortcuts when the input and the output are of the same dimensions. Dotted lines represent the shortcuts when the dimensions increase. There are options to compensate for the increase in dimensions:
- (A) The shortcut still performs identity mapping with extra zero padding
- (B) The projection shortcut is used for increasing dimensions (using \(1 \times 1\) convolutions)
- (C) All shortcuts are projections
For the ResNet34, the convolutional layers mostly have \(3 \times 3\) filters. For the same feature map size, the layers have the same number of filters. If the feature map size is halved, the number of filters is doubled. The downsampling is done by convolution with stride of 2. When shortcuts go across feature maps of two sizes, the feature maps are computed with a stride of 2. At the end of the network there is a global average pooling and a 1000-way fully connected layer with softmax. The total number of layers is 34.
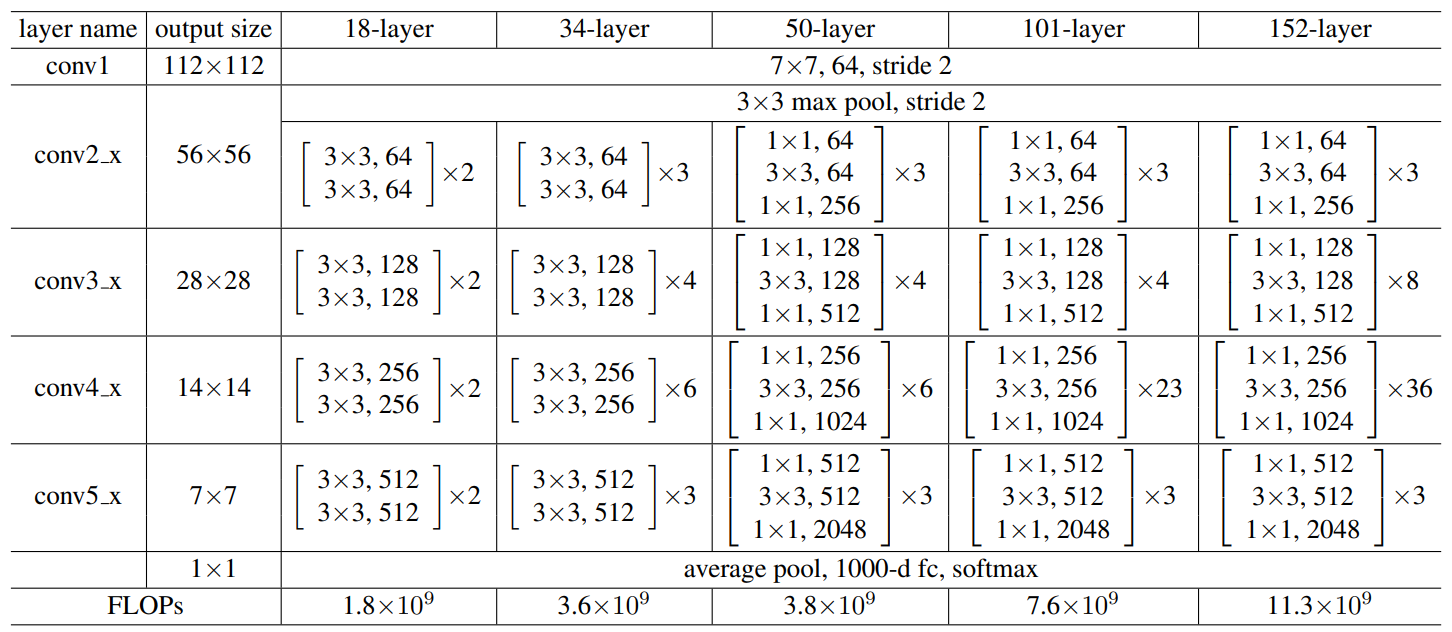
Bottleneck architecture
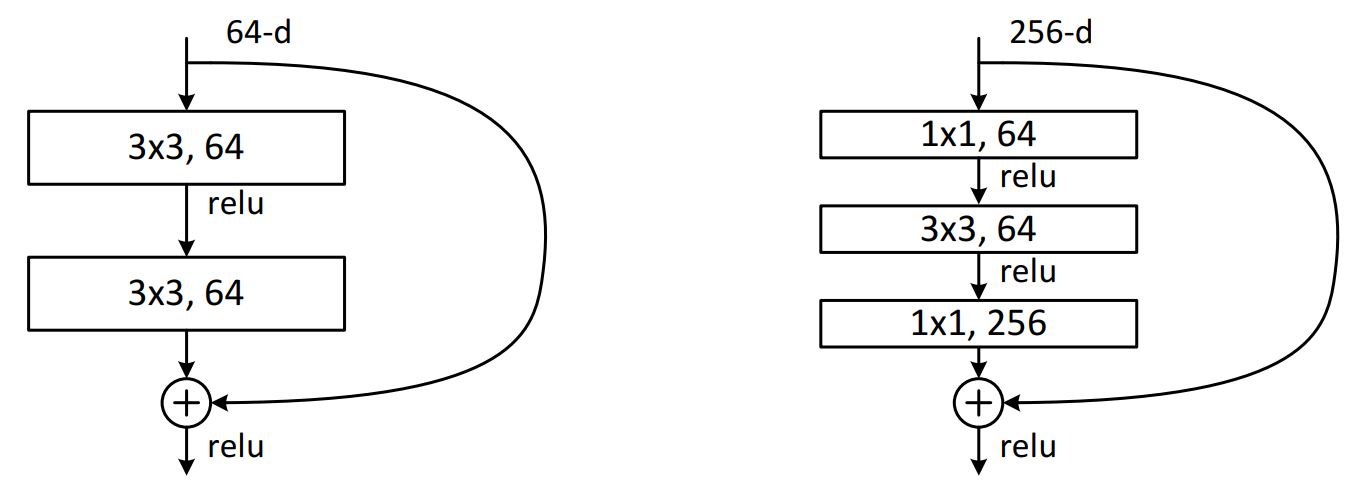
For deeper networks, a modification of the building block is used, referred to as a bottleneck design. For each residual function \(F\), a stack of 3 layers is used instead of 2. The three layers are \(1 \times 1\), \(3 \times 3\), \(1 \times 1\) convolutions, where \(1 \times 1\) layers are responsible for reducing and then restoring dimensions, leaving the \(3 \times 3\) layer a bottleneck with smaller input/output dimensions.
Both designs below have similar time complexity. The parameter-free identity shortcuts are particularly important for the bottleneck architectures. If the projections are used for the shortcuts, the complexity and model size are doubled.
Implementation
For ImageNet dataset, the image is resized with its shorter side randomly sampled in \([256,480]\) for scale augmentation. A \(224 \times 224\) crop is randomly sampled from an image or its horizontal flip, with the per-pixel mean subtracted. The standard color augementation is used as in AlexNet paper. Batch normalization is applied. The solver used is SGD with a batch size of 256. The learning rate starts from 0.1 and is divided by 10 when the error plateaus. The models are trained for up to \(60 \times 10^4\) iterations. The weight decay is 0.0001 and momentum 0.9. Dropout is not used. For testing, a standard 10-crop testing is used as in the AlexNet paper.
Code
import tensorflow.compat.v2 as tf
from keras import backend
from keras.applications import imagenet_utils
from keras.engine import training
from keras.layers import VersionAwareLayers
from keras.utils import data_utils
from keras.utils import layer_utils
from tensorflow.python.util.tf_export import keras_export
layers = None
def ResNet(stack_fn,
preact,
use_bias,
model_name='resnet',
include_top=True,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000,
classifier_activation='softmax',
**kwargs):
"""Instantiates the ResNet, ResNetV2, and ResNeXt architecture.
Args:
stack_fn: a function that returns output tensor for the
stacked residual blocks.
preact: whether to use pre-activation or not
(True for ResNetV2, False for ResNet and ResNeXt).
use_bias: whether to use biases for convolutional layers or not
(True for ResNet and ResNetV2, False for ResNeXt).
model_name: string, model name.
include_top: whether to include the fully-connected
layer at the top of the network.
weights: one of `None` (random initialization),
'imagenet' (pre-training on ImageNet),
or the path to the weights file to be loaded.
input_tensor: optional Keras tensor
(i.e. output of `layers.Input()`)
to use as image input for the model.
input_shape: optional shape tuple, only to be specified
if `include_top` is False (otherwise the input shape
has to be `(224, 224, 3)` (with `channels_last` data format)
or `(3, 224, 224)` (with `channels_first` data format).
It should have exactly 3 inputs channels.
pooling: optional pooling mode for feature extraction
when `include_top` is `False`.
- `None` means that the output of the model will be
the 4D tensor output of the
last convolutional layer.
- `avg` means that global average pooling
will be applied to the output of the
last convolutional layer, and thus
the output of the model will be a 2D tensor.
- `max` means that global max pooling will
be applied.
classes: optional number of classes to classify images
into, only to be specified if `include_top` is True, and
if no `weights` argument is specified.
classifier_activation: A `str` or callable. The activation function to use
on the "top" layer. Ignored unless `include_top=True`. Set
`classifier_activation=None` to return the logits of the "top" layer.
When loading pretrained weights, `classifier_activation` can only
be `None` or `"softmax"`.
**kwargs: For backwards compatibility only.
Returns:
A `keras.Model` instance.
"""
global layers
if 'layers' in kwargs:
layers = kwargs.pop('layers')
else:
layers = VersionAwareLayers()
if kwargs:
raise ValueError('Unknown argument(s): %s' % (kwargs,))
if not (weights in {'imagenet', None} or tf.io.gfile.exists(weights)):
raise ValueError('The `weights` argument should be either '
'`None` (random initialization), `imagenet` '
'(pre-training on ImageNet), '
'or the path to the weights file to be loaded.')
if weights == 'imagenet' and include_top and classes != 1000:
raise ValueError('If using `weights` as `"imagenet"` with `include_top`'
' as true, `classes` should be 1000')
# Determine proper input shape
input_shape = imagenet_utils.obtain_input_shape(
input_shape,
default_size=224,
min_size=32,
data_format=backend.image_data_format(),
require_flatten=include_top,
weights=weights)
if input_tensor is None:
img_input = layers.Input(shape=input_shape)
else:
if not backend.is_keras_tensor(input_tensor):
img_input = layers.Input(tensor=input_tensor, shape=input_shape)
else:
img_input = input_tensor
bn_axis = 3 if backend.image_data_format() == 'channels_last' else 1
x = layers.ZeroPadding2D(
padding=((3, 3), (3, 3)), name='conv1_pad')(img_input)
x = layers.Conv2D(64, 7, strides=2, use_bias=use_bias, name='conv1_conv')(x)
if not preact:
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name='conv1_bn')(x)
x = layers.Activation('relu', name='conv1_relu')(x)
x = layers.ZeroPadding2D(padding=((1, 1), (1, 1)), name='pool1_pad')(x)
x = layers.MaxPooling2D(3, strides=2, name='pool1_pool')(x)
x = stack_fn(x)
if preact:
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name='post_bn')(x)
x = layers.Activation('relu', name='post_relu')(x)
if include_top:
x = layers.GlobalAveragePooling2D(name='avg_pool')(x)
imagenet_utils.validate_activation(classifier_activation, weights)
x = layers.Dense(classes, activation=classifier_activation,
name='predictions')(x)
else:
if pooling == 'avg':
x = layers.GlobalAveragePooling2D(name='avg_pool')(x)
elif pooling == 'max':
x = layers.GlobalMaxPooling2D(name='max_pool')(x)
# Ensure that the model takes into account
# any potential predecessors of `input_tensor`.
if input_tensor is not None:
inputs = layer_utils.get_source_inputs(input_tensor)
else:
inputs = img_input
# Create model.
model = training.Model(inputs, x, name=model_name)
# Load weights.
if (weights == 'imagenet') and (model_name in WEIGHTS_HASHES):
if include_top:
file_name = model_name + '_weights_tf_dim_ordering_tf_kernels.h5'
file_hash = WEIGHTS_HASHES[model_name][0]
else:
file_name = model_name + '_weights_tf_dim_ordering_tf_kernels_notop.h5'
file_hash = WEIGHTS_HASHES[model_name][1]
weights_path = data_utils.get_file(
file_name,
BASE_WEIGHTS_PATH + file_name,
cache_subdir='models',
file_hash=file_hash)
model.load_weights(weights_path)
elif weights is not None:
model.load_weights(weights)
return model
def block1(x, filters, kernel_size=3, stride=1, conv_shortcut=True, name=None):
"""A residual block.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer.
kernel_size: default 3, kernel size of the bottleneck layer.
stride: default 1, stride of the first layer.
conv_shortcut: default True, use convolution shortcut if True,
otherwise identity shortcut.
name: string, block label.
Returns:
Output tensor for the residual block.
"""
bn_axis = 3 if backend.image_data_format() == 'channels_last' else 1
if conv_shortcut:
shortcut = layers.Conv2D(
4 * filters, 1, strides=stride, name=name + '_0_conv')(x)
shortcut = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_0_bn')(shortcut)
else:
shortcut = x
x = layers.Conv2D(filters, 1, strides=stride, name=name + '_1_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_1_bn')(x)
x = layers.Activation('relu', name=name + '_1_relu')(x)
x = layers.Conv2D(
filters, kernel_size, padding='SAME', name=name + '_2_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_2_bn')(x)
x = layers.Activation('relu', name=name + '_2_relu')(x)
x = layers.Conv2D(4 * filters, 1, name=name + '_3_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_3_bn')(x)
x = layers.Add(name=name + '_add')([shortcut, x])
x = layers.Activation('relu', name=name + '_out')(x)
return x
def stack1(x, filters, blocks, stride1=2, name=None):
"""A set of stacked residual blocks.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer in a block.
blocks: integer, blocks in the stacked blocks.
stride1: default 2, stride of the first layer in the first block.
name: string, stack label.
Returns:
Output tensor for the stacked blocks.
"""
x = block1(x, filters, stride=stride1, name=name + '_block1')
for i in range(2, blocks + 1):
x = block1(x, filters, conv_shortcut=False, name=name + '_block' + str(i))
return x
def block2(x, filters, kernel_size=3, stride=1, conv_shortcut=False, name=None):
"""A residual block.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer.
kernel_size: default 3, kernel size of the bottleneck layer.
stride: default 1, stride of the first layer.
conv_shortcut: default False, use convolution shortcut if True,
otherwise identity shortcut.
name: string, block label.
Returns:
Output tensor for the residual block.
"""
bn_axis = 3 if backend.image_data_format() == 'channels_last' else 1
preact = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_preact_bn')(x)
preact = layers.Activation('relu', name=name + '_preact_relu')(preact)
if conv_shortcut:
shortcut = layers.Conv2D(
4 * filters, 1, strides=stride, name=name + '_0_conv')(preact)
else:
shortcut = layers.MaxPooling2D(1, strides=stride)(x) if stride > 1 else x
x = layers.Conv2D(
filters, 1, strides=1, use_bias=False, name=name + '_1_conv')(preact)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_1_bn')(x)
x = layers.Activation('relu', name=name + '_1_relu')(x)
x = layers.ZeroPadding2D(padding=((1, 1), (1, 1)), name=name + '_2_pad')(x)
x = layers.Conv2D(
filters,
kernel_size,
strides=stride,
use_bias=False,
name=name + '_2_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_2_bn')(x)
x = layers.Activation('relu', name=name + '_2_relu')(x)
x = layers.Conv2D(4 * filters, 1, name=name + '_3_conv')(x)
x = layers.Add(name=name + '_out')([shortcut, x])
return x
def stack2(x, filters, blocks, stride1=2, name=None):
"""A set of stacked residual blocks.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer in a block.
blocks: integer, blocks in the stacked blocks.
stride1: default 2, stride of the first layer in the first block.
name: string, stack label.
Returns:
Output tensor for the stacked blocks.
"""
x = block2(x, filters, conv_shortcut=True, name=name + '_block1')
for i in range(2, blocks):
x = block2(x, filters, name=name + '_block' + str(i))
x = block2(x, filters, stride=stride1, name=name + '_block' + str(blocks))
return x
def block3(x,
filters,
kernel_size=3,
stride=1,
groups=32,
conv_shortcut=True,
name=None):
"""A residual block.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer.
kernel_size: default 3, kernel size of the bottleneck layer.
stride: default 1, stride of the first layer.
groups: default 32, group size for grouped convolution.
conv_shortcut: default True, use convolution shortcut if True,
otherwise identity shortcut.
name: string, block label.
Returns:
Output tensor for the residual block.
"""
bn_axis = 3 if backend.image_data_format() == 'channels_last' else 1
if conv_shortcut:
shortcut = layers.Conv2D(
(64 // groups) * filters,
1,
strides=stride,
use_bias=False,
name=name + '_0_conv')(x)
shortcut = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_0_bn')(shortcut)
else:
shortcut = x
x = layers.Conv2D(filters, 1, use_bias=False, name=name + '_1_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_1_bn')(x)
x = layers.Activation('relu', name=name + '_1_relu')(x)
c = filters // groups
x = layers.ZeroPadding2D(padding=((1, 1), (1, 1)), name=name + '_2_pad')(x)
x = layers.DepthwiseConv2D(
kernel_size,
strides=stride,
depth_multiplier=c,
use_bias=False,
name=name + '_2_conv')(x)
x_shape = backend.shape(x)[:-1]
x = backend.reshape(x, backend.concatenate([x_shape, (groups, c, c)]))
x = layers.Lambda(
lambda x: sum(x[:, :, :, :, i] for i in range(c)),
name=name + '_2_reduce')(x)
x = backend.reshape(x, backend.concatenate([x_shape, (filters,)]))
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_2_bn')(x)
x = layers.Activation('relu', name=name + '_2_relu')(x)
x = layers.Conv2D(
(64 // groups) * filters, 1, use_bias=False, name=name + '_3_conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_3_bn')(x)
x = layers.Add(name=name + '_add')([shortcut, x])
x = layers.Activation('relu', name=name + '_out')(x)
return x
def stack3(x, filters, blocks, stride1=2, groups=32, name=None):
"""A set of stacked residual blocks.
Args:
x: input tensor.
filters: integer, filters of the bottleneck layer in a block.
blocks: integer, blocks in the stacked blocks.
stride1: default 2, stride of the first layer in the first block.
groups: default 32, group size for grouped convolution.
name: string, stack label.
Returns:
Output tensor for the stacked blocks.
"""
x = block3(x, filters, stride=stride1, groups=groups, name=name + '_block1')
for i in range(2, blocks + 1):
x = block3(
x,
filters,
groups=groups,
conv_shortcut=False,
name=name + '_block' + str(i))
return x
def ResNet50(include_top=True,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000,
**kwargs):
"""Instantiates the ResNet50 architecture."""
def stack_fn(x):
x = stack1(x, 64, 3, stride1=1, name='conv2')
x = stack1(x, 128, 4, name='conv3')
x = stack1(x, 256, 6, name='conv4')
return stack1(x, 512, 3, name='conv5')
return ResNet(stack_fn, False, True, 'resnet50', include_top, weights,
input_tensor, input_shape, pooling, classes, **kwargs)
def ResNet101(include_top=True,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000,
**kwargs):
"""Instantiates the ResNet101 architecture."""
def stack_fn(x):
x = stack1(x, 64, 3, stride1=1, name='conv2')
x = stack1(x, 128, 4, name='conv3')
x = stack1(x, 256, 23, name='conv4')
return stack1(x, 512, 3, name='conv5')
return ResNet(stack_fn, False, True, 'resnet101', include_top, weights,
input_tensor, input_shape, pooling, classes, **kwargs)
@keras_export('keras.applications.resnet.ResNet152',
'keras.applications.ResNet152')
def ResNet152(include_top=True,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000,
**kwargs):
"""Instantiates the ResNet152 architecture."""
def stack_fn(x):
x = stack1(x, 64, 3, stride1=1, name='conv2')
x = stack1(x, 128, 8, name='conv3')
x = stack1(x, 256, 36, name='conv4')
return stack1(x, 512, 3, name='conv5')
return ResNet(stack_fn, False, True, 'resnet152', include_top, weights,
input_tensor, input_shape, pooling, classes, **kwargs)