Densely Connected Convolutional Networks
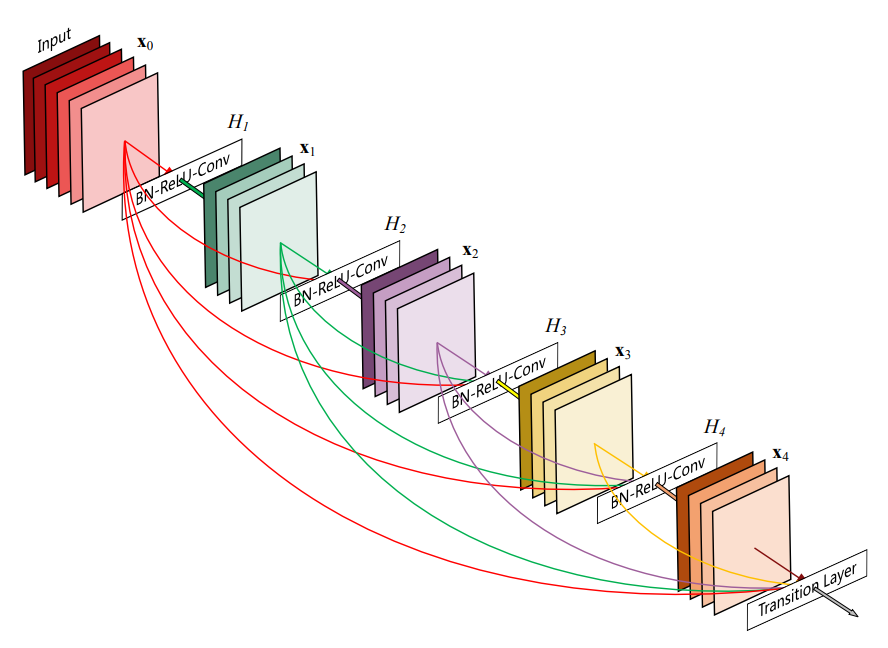
The general idea of the Densely Connected Convolutional Networks (DenseNet) is to connect each layer to every subsequent layer in a feed-forward convolutional neural network (CNN), such that the number of incoming connections for each layer grows as the arithmetic sequence $1,2,3,\ldots,L$, where $L$ is the number of layers in the network. Therefore, the number of connections between layers in the DenseNet is
$$\frac{L(L+1)}{2}$$
In practice, however, the number of such connections are limited to a block of layers with the same feature map size. DenseNet has the following advantages over other architectures (general CNN's, ResNet and FractalNet): 1. Solving the vanishing-gradient problem 2. Better feature propagation 3. Encouraging feature reuse 4. Reducing the number of parameters
Intuition
DenseNet connects all layers directly with each other (within a block where each layer has the same feature map size). In contrast to ResNet's, the features are not combined through summation before they are passed into a layer. Instead, features are concatenated. Therefore, $l^{\text{th}}$ layer has $l$ inputs of the feature maps of all preceding layers within the dense block. Its own feature maps are passed on to all $(L-l)$ subsequent layers.
DenseNet requires fewer parameters than traditional CNN's because there is no need to relearn redundant feature maps. Traditional feed-forward architectures read the state from the previous layer and write to the subsequent layer, changing its state but also adding the information that needs to be preserved (hence the growing number of feature maps in the subsequent layers). DenseNet explicitly differentiates between added and preserved information in the network, adding only a small set of feature maps to the collective knowledge of the network. The final classifier makes a decision based on all feature maps in the network.
Because each layer has a direct access to the gradients from the loss function and the original input signal (implicit deep supervision), the gradients are propagated more efficiently.
Inspiration
Highway Networks and ResNets show that bypassing paths are essential for training very deep networks. GoogleNet uses concatenation of feature maps of different sizes to increase the network width. ResNet in ResNet shows that if the depth is sufficient, increasing the number of filters in each layer improves the performance of the network. ResNets with stochastic depth show that many layers don't contribute much to the final decision made by the classifier so that some of them can be dropped at random. Network in Network (NIN) extracts more complicated features by including micro multi-layer perceptrons (MLP) into the filters of convolutional layers. Deeply-Fused Network (DFN) improves information flow by combining intermediate layers of different base networks.
Comparison
Comparing with ResNets, DenseNets concatenate feature maps learned by different layers which increases variation in the input of subsequent layers and increases efficiency. Comparing with Inception networks, DenseNets are simpler and easier to train.
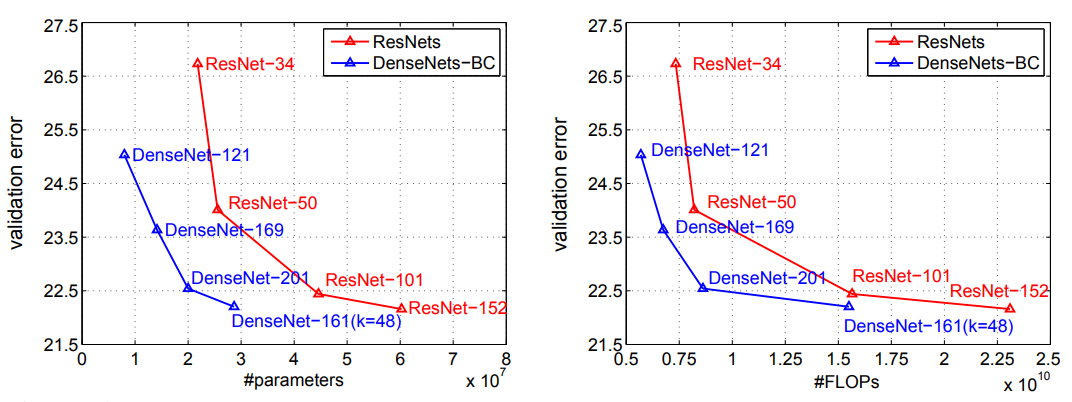
Architecture
The network has $L$ layers, each implementing a non-linear transformation $H_l(\cdot)$, where $l$ is the index of a layer. Let $x_0$ be the input image and $x_l$ the output of the $l^{\text{th}}$ layer.
Traditional CNNs connect the output of the $l^{\text{th}}$ layer as input to the $(l+1)^{\text{th}}$ layer:
$$x_l = H_l(x_{l-1})$$
ResNets add a skip-connection that bypasses the non-linear transformation with an identity function:
$$x_l = H_l(x_{l-1}) + x_{l-1}$$

In a DenseNet, $l$ layer receives the feature maps of all preceding layers $x_0,x_1,\ldots,x_{l-1}$, concatenated together into a single tensor as input:
$$x_l = H_l([x_0,x_1,\ldots,x_{l-1}])$$
$H_l(\cdot)$ is a composite function of three consecutive operations: batch normalization (BN), followed by a rectified linear unit (ReLU), and a $3 \times 3$ convolution (Conv) with 1px zero-padding and stride 1.
The concatenation of feature maps has to be done with the feature maps of the same size. However, an essential part of convolutional networks is down-sampling layers that change the size of feature maps. Therefore, the architecture is divided into dense blocks with feature maps of the same size. Transition layers are the layers between the dense blocks. Transition layers consist of BN layer, ReLU activation, a $1 \times 1$ Conv layer followed by a $2 \times 2$ average pooling layer.
If each function $H_l$ produces $k$ feature maps, the $l^{\text{th}}$ layer has $k_0 + k \times (l-1)$, where $k_0$ is the number of channels in the input layer. The hyper-parameter $k$ is defined as the growth rate of the network.
Feature maps can be viewed as the global state of the network. Each layer adds $k$ feature maps of its own to the state. The growth rate regulates how much new information each layer contributes to the global state.
Improvements
In order to reduce the number of input feature maps (and thus efficiency), a $1 \times 1$ Conv is introduced as a bottleneck layer. The modified version of $H_l(\cdot)$ with a bottleneck layer has BN-ReLU-Conv(1x1)-BN-ReLU-Conv(3x3) structure, and the network is referred to as DenseNet-B. Each $1 \times 1$ convolution produces $4k$ feature maps.
Let $m$ be the number of feature maps in a dense block. The hyper-parameter $0 \lt \theta \le 1$ is referred to as the compression factor such that the transition layer generates $\theta m$ feature maps. If both bottleneck and transition layers with $\theta \lt 1$ are used, the model is referred to as DenseNet-BC.
Feature reuse
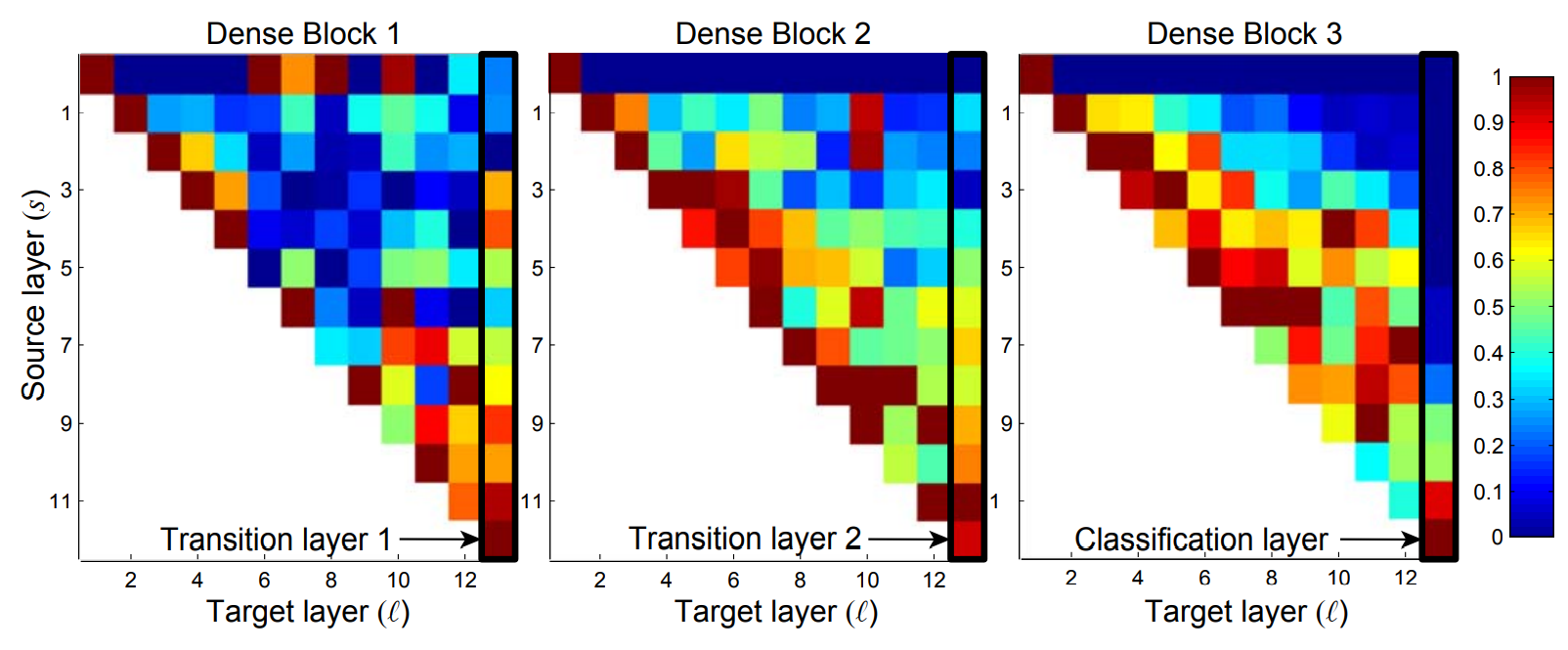
DenseNets allow layers to access feature maps of the previous layers directly within the same dense block or indirectly through transition layers. For a DenseNet trained on augmented CIFAR-10 with $L=40$ and $k=12$, a heat-map for all three dense blocks is constructed. Each square represents a convolutional layer $l$ within a block, and the color encodes the average $L1$ norm (normalized by the number of input feature-maps) of weights connecting layer $s$ to layer $l$ within a dense block. It depicts the dependency of a convolutional layer on its preceding layers. The first row encodes weights connected to the input layer of the dense block.
Observations from the plot: 1. All layers spread weights over many inputs, demonstrating that the features are indeed reused throughout the dense block. 2. Transition layers also spread their weights across all layers within the preceding dense block, indicating information flow. 3. The layers within the second and third dense block assign least weights to the outputs of the transition layer, signifying that many transition layer outputs are redundant. 4. The final classification layer concentrates on the final feature maps, suggesting there are more high-level features produced late in the network.
Implementation
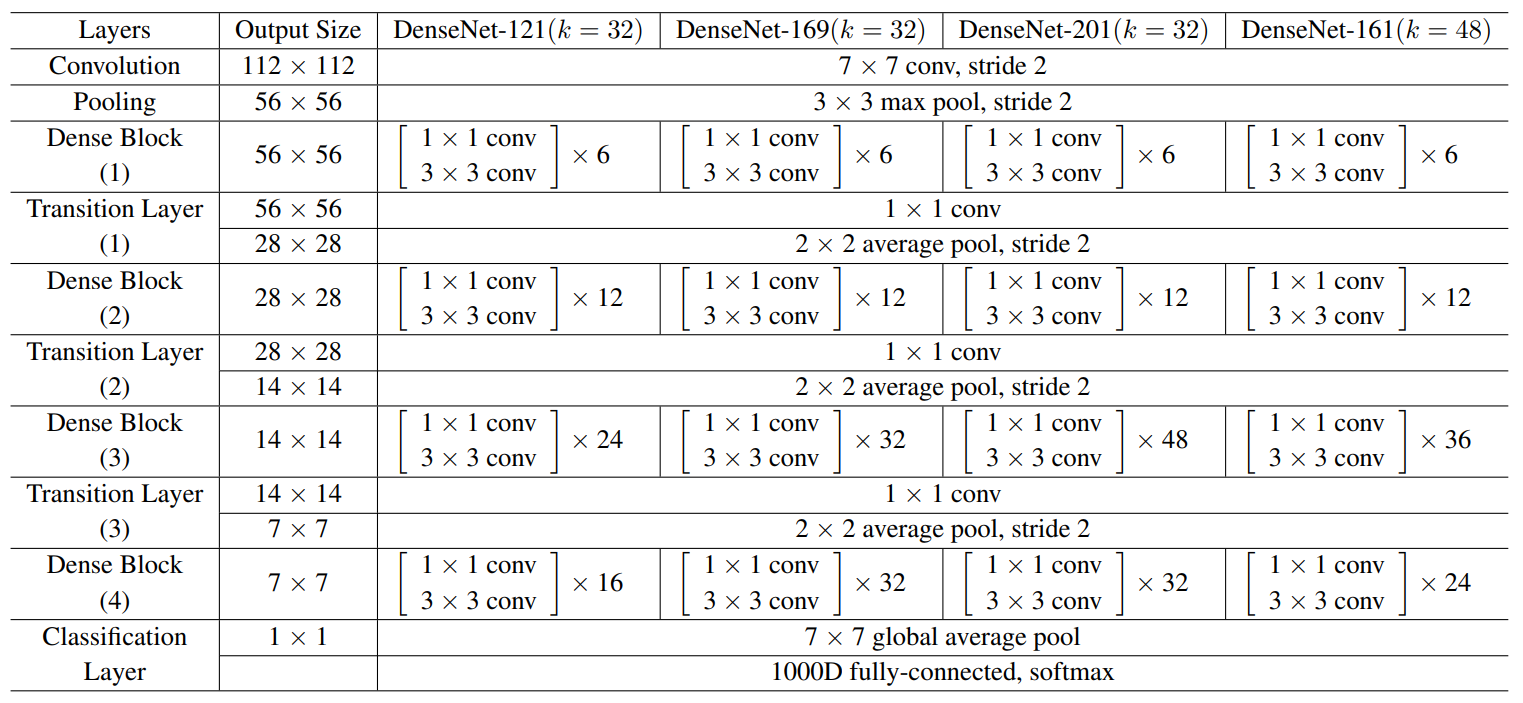
In the experiments, DenseNet has three dense blocks (four dense blocks for ImageNet) that each has an equal number of layers. Before entering the first dense block, a convolution with 16 (or $2k$ for DenseNet-BC) $7 \times 7$ kernels with stride 2 is performed on the input images. At the end of the last dense block, a global average pooling is performed and then a softmax classifier is attached. The feature map sizes in the three dense blocks are $32 \times 32$, $16 \times 16$, and $8 \times 8$.
Code
import tensorflow as tf
from tensorflow.keras import layers
def dense_block(x, blocks, growth_rate, name):
"""A dense block.
Args:
x: input tensor.
blocks: integer, the number of building blocks.
name: string, block label.
Returns:
Output tensor for the block.
"""
for i in range(blocks):
x = conv_block(x, growth_rate, name=name + '_block' + str(i + 1))
return x
def conv_block(x, growth_rate, name):
"""A building block for a dense block.
Args:
x: input tensor.
growth_rate: float, growth rate at dense layers.
name: string, block label.
Returns:
Output tensor for the block.
"""
bn_axis = -1
x1 = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_0_bn')(
x)
x1 = layers.Activation('relu', name=name + '_0_relu')(x1)
x1 = layers.Conv2D(
4 * growth_rate, 1, use_bias=False, name=name + '_1_conv')(
x1)
x1 = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_1_bn')(
x1)
x1 = layers.Activation('relu', name=name + '_1_relu')(x1)
x1 = layers.Conv2D(
growth_rate, 3, padding='same', use_bias=False, name=name + '_2_conv')(
x1)
x = layers.Concatenate(axis=bn_axis, name=name + '_concat')([x, x1])
return x
def transition_block(x, reduction, name):
"""A transition block.
Args:
x: input tensor.
reduction: float, compression rate at transition layers.
name: string, block label.
Returns:
output tensor for the block.
"""
bn_axis = -1
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name=name + '_bn')(
x)
x = layers.Activation('relu', name=name + '_relu')(x)
x = layers.Conv2D(
int(backend.int_shape(x)[bn_axis] * reduction),
1,
use_bias=False,
name=name + '_conv')(
x)
x = layers.AveragePooling2D(2, strides=2, name=name + '_pool')(x)
return x
def DenseNet(
blocks,
growth_rate=32,
include_top=True,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000,
classifier_activation='softmax'):
"""Instantiates the DenseNet architecture.
Reference:
- [Densely Connected Convolutional Networks](
https://arxiv.org/abs/1608.06993) (CVPR 2017)
Args:
blocks: numbers of building blocks for the four dense layers.
include_top: whether to include the fully-connected
layer at the top of the network.
weights: one of `None` (random initialization),
'imagenet' (pre-training on ImageNet),
or the path to the weights file to be loaded.
input_tensor: optional Keras tensor
(i.e. output of `layers.Input()`)
to use as image input for the model.
input_shape: optional shape tuple, only to be specified
if `include_top` is False (otherwise the input shape
has to be `(224, 224, 3)` (with `'channels_last'` data format)
or `(3, 224, 224)` (with `'channels_first'` data format).
It should have exactly 3 inputs channels,
and width and height should be no smaller than 32.
E.g. `(200, 200, 3)` would be one valid value.
pooling: optional pooling mode for feature extraction
when `include_top` is `False`.
- `None` means that the output of the model will be
the 4D tensor output of the
last convolutional block.
- `avg` means that global average pooling
will be applied to the output of the
last convolutional block, and thus
the output of the model will be a 2D tensor.
- `max` means that global max pooling will
be applied.
classes: optional number of classes to classify images
into, only to be specified if `include_top` is True, and
if no `weights` argument is specified.
classifier_activation: A `str` or callable. The activation function to use
on the "top" layer. Ignored unless `include_top=True`. Set
`classifier_activation=None` to return the logits of the "top" layer.
When loading pretrained weights, `classifier_activation` can only
be `None` or `"softmax"`.
Returns:
A `keras.Model` instance.
"""
# Determine proper input shape
input_shape = imagenet_utils.obtain_input_shape(
input_shape,
default_size=224,
min_size=32,
data_format=backend.image_data_format(),
require_flatten=include_top,
weights=weights)
input_shape = (32,32,3)
if input_tensor is None:
img_input = layers.Input(shape=input_shape)
else:
if not backend.is_keras_tensor(input_tensor):
img_input = layers.Input(tensor=input_tensor, shape=input_shape)
else:
img_input = input_tensor
bn_axis = -1
x = layers.ZeroPadding2D(padding=((3, 3), (3, 3)))(img_input)
x = layers.Conv2D(2*growth_rate, 7, strides=2, use_bias=False, name='conv1/conv')(x)
x = layers.BatchNormalization(
axis=bn_axis, epsilon=1.001e-5, name='conv1/bn')(
x)
x = layers.Activation('relu', name='conv1/relu')(x)
x = layers.ZeroPadding2D(padding=((1, 1), (1, 1)))(x)
x = layers.MaxPooling2D(3, strides=2, name='pool1')(x)
x = dense_block(x, growth_rate, blocks[0], name='conv2')
x = transition_block(x, 0.5, name='pool2')
x = dense_block(x, growth_rate, blocks[1], name='conv3')
x = transition_block(x, 0.5, name='pool3')
x = dense_block(x, growth_rate, blocks[2], name='conv4')
x = transition_block(x, 0.5, name='pool4')
x = dense_block(x, growth_rate, blocks[3], name='conv5')
x = layers.BatchNormalization(axis=bn_axis, epsilon=1.001e-5, name='bn')(x)
x = layers.Activation('relu', name='relu')(x)
if include_top:
x = layers.GlobalAveragePooling2D(name='avg_pool')(x)
x = layers.Dense(classes, activation=classifier_activation,
name='predictions')(x)
else:
if pooling == 'avg':
x = layers.GlobalAveragePooling2D(name='avg_pool')(x)
elif pooling == 'max':
x = layers.GlobalMaxPooling2D(name='max_pool')(x)
# Ensure that the model takes into account
# any potential predecessors of `input_tensor`.
if input_tensor is not None:
inputs = layer_utils.get_source_inputs(input_tensor)
else:
inputs = img_input
# Create model.
if blocks == [6, 12, 24, 16]:
model = training.Model(inputs, x, name='DenseNet-121')
elif blocks == [6, 12, 32, 32]:
model = training.Model(inputs, x, name='DenseNet-169')
elif blocks == [6, 12, 48, 32]:
model = training.Model(inputs, x, name='DenseNet-201')
elif blocks == [6, 12, 36, 24]:
model = training.Model(inputs, x, name='DenseNet-161')
else:
model = training.Model(inputs, x, name='DenseNet')
return model
def DenseNet121(include_top=True,
growth_rate=32,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000):
"""Instantiates the Densenet121 architecture."""
return DenseNet([6, 12, 24, 16], include_top, weights, input_tensor,
input_shape, pooling, classes)
def DenseNet169(include_top=True,
growth_rate=32,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000):
"""Instantiates the Densenet169 architecture."""
return DenseNet([6, 12, 32, 32], include_top, weights, input_tensor,
input_shape, pooling, classes)
def DenseNet201(include_top=True,
growth_rate=32,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000):
"""Instantiates the Densenet201 architecture."""
return DenseNet([6, 12, 48, 32], include_top, weights, input_tensor,
input_shape, pooling, classes)
def DenseNet161(include_top=True,
growth_rate=48,
weights='imagenet',
input_tensor=None,
input_shape=None,
pooling=None,
classes=1000):
"""Instantiates the Densenet161 architecture."""
return DenseNet([6, 12, 36, 24], include_top, weights, input_tensor,
input_shape, pooling, classes)
def decode_predictions(preds, top=5):
return imagenet_utils.decode_predictions(preds, top=top)